Basics

We introduce basic notions here. Let us have a look at Fig. 3.

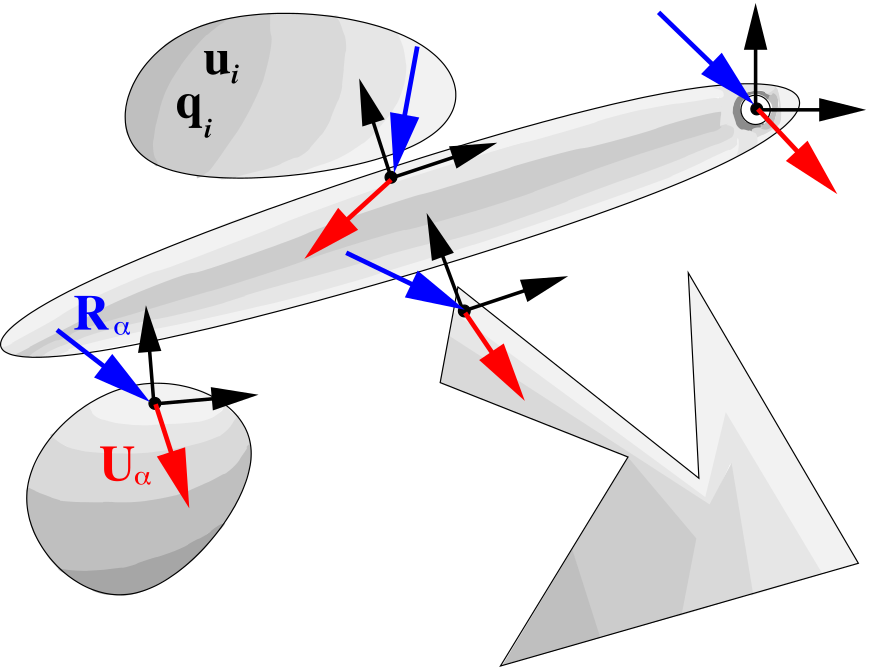
Fig. 3 A multi–body domain.

There are four bodies in the figure. Placement of each point of every body is determined by a configuration \(\mathbf{q}_{i}\). Velocity of each point of every body is determined by a velocity \(\mathbf{u}_{i}\). Let \(\mathbf{q}\) and \(\mathbf{u}\) collect configurations and velocities of all bodies. If the time history of velocity is known, the configuration time history can be computed as

(1)\[\mathbf{q}\left(t\right)=\mathbf{q}\left(0\right)+\int_{0}^{t}\mathbf{u}dt\]

The velocity is determined by integrating Newton’s law

(2)\[\mathbf{u}\left(t\right)=\mathbf{u}\left(0\right)+\mathbf{M}^{-1}\int_{0}^{t}\left(\mathbf{f}+\mathbf{H}^{T}\mathbf{R}\right)dt\]

where \(\mathbf{M}\) is an inertia operator (assumed constant here), \(\mathbf{f}\) is an out of balance force, \(\mathbf{H}\) is a linear operator, and \(\mathbf{R}\) collects some point forces \(\mathbf{R}_{\alpha}\). While integrating the motion of bodies, we keep track of a number of local coordinate systems (local frames). There are four of them in the above figure. Each local frame is related to a pair of points, usually belonging to two distinct bodies. An observer embedded at a local frame calculates the local relative velocity \(\mathbf{U}_{\alpha}\) of one of the points, viewed from the perspective of the other point. Let \(\mathbf{U}\) collect all local velocities. Then, we can find a linear transformation \(\mathbf{H}\), such that

(3)\[\mathbf{U}=\mathbf{H}\mathbf{u}\]

In our case local frames correspond to constraints. We influence the local relative velocities by applying local forces \(\mathbf{R}_{\alpha}\). This can be collectively described by an implicit relation

(4)\[\mathbf{C}\left(\mathbf{U},\mathbf{R}\right)=\mathbf{0}\]

Hence, in order to integrate equations (1) and (2), at every instant of time we need to solve the implicit relation (4). Here is an example of a numerical approximation of such procedure

(5)\[\mathbf{q}^{t+\frac{h}{2}}=\mathbf{q}^{t}+\frac{h}{2}\mathbf{u}^{t}\]

(6)\[\mathbf{u}^{t+h}=\mathbf{u}^{t}+\mathbf{M}^{-1}h\mathbf{f}^{t+\frac{h}{2}}+\mathbf{M}^{-1}\mathbf{H}^{T}\mathbf{R}\]

(7)\[\mathbf{q}^{t+h}=\mathbf{q}^{t+\frac{h}{2}}+\frac{h}{2}\mathbf{u}^{t+h}\]

where \(h\) is a discrete time step. As the time step h does not appear by \(\mathbf{M}^{-1}\mathbf{H}^{T}\mathbf{R}\), \(\mathbf{R}\) should now be interpreted as an impulse (an integral of reactions over \(\left[t,t+h\right]\)). At a start we have

(8)\[\mathbf{q}^{0}\mbox{ and }\mathbf{u}^{0}\mbox{ as prescribed initial conditions.}\]

The out of balance force

\[\mathbf{f}^{t+\frac{h}{2}}=\mathbf{f}\left(\mathbf{q}^{t+\frac{h}{2}},t+\frac{h}{2}\right)\]

incorporates both internal and external forces. The symmetric and positive-definite inertia operator

\[\mathbf{M}=\mathbf{M}\left(\mathbf{q}^{0}\right)\]

is computed once. The linear operator

\[\mathbf{H}=\mathbf{H}\left(\mathbf{q}^{t+\frac{h}{2}}\right)\]

is computed at every time step. The number of rows of \(\mathbf{H}\) depends on the number of constraints, while its rank is related to their linear independence. We then compute

\[\mathbf{B}=\mathbf{H}\left(\mathbf{u}^{t}+\mathbf{M}^{-1}h\mathbf{f}^{t+\frac{h}{2}}\right)\]

and

(9)\[\mathbf{W}=\mathbf{H}\mathbf{M}^{-1}\mathbf{H}^{T}\]

which is symmetric and semi-positive definite. The linear transformation

(10)\[\mathbf{U}=\mathbf{B}+\mathbf{W}\mathbf{R}\]

maps constraint reactions \(\mathbf{R}\) into local relative velocities \(\mathbf{U}=\mathbf{H}\mathbf{u}^{t+h}\) at time \(t+h\). Relation (84) will be here referred to as the local dynamics. Finally

(11)\[\mathbf{R}\mbox{ is such that }\mathbf{C}\left(\mathbf{U},\mathbf{R}\right)= \mathbf{C}\left(\mathbf{B}+\mathbf{W}\mathbf{R},\mathbf{R}\right)= \mathbf{C}\left(\mathbf{R}\right)=\mathbf{0}\]

where \(\mathbf{C}\) is a nonlinear and usually nonsmooth operator. A basic Contact Dynamics algorithm can be summarised as follows:

1. Perform first half–step \(\mathbf{q}^{t+\frac{h}{2}}=\mathbf{q}^{t}+\frac{h}{2}\mathbf{u}^{t}\).

2. Update existing constraints and detect new contact points.

3. Compute \(\mathbf{W}\), \(\mathbf{B}\).

4. Solve \(\mathbf{C}\left(\mathbf{R}\right)=\mathbf{0}\).

5. Update velocity \(\mathbf{u}^{t+h}=\mathbf{u}^{t}+\mathbf{M}^{-1}h\mathbf{f}^{t+\frac{h}{2}}+\mathbf{M}^{-1}\mathbf{H}^{T}\mathbf{R}\).

6. Perform second half–step \(\mathbf{q}^{t+h}=\mathbf{q}^{t+\frac{h}{2}}+\frac{h}{2}\mathbf{u}^{t+h}\).

It should be emphasized that the above presentation exemplifies only a particular instance among many available variants of Contact Dynamics.