Pinned bar

Reference: W. G. McLean, E. W. Nelson, C. L. Best, Schaum’s Outline of Theory and Problems Reference: of Engineering Mechanics, Statics and Dynamics, McGraw-Hill Book Co., Inc., New York, NY, 1978, p. 336.
Analysis: Explicit dynamics, bilaterally constrained motion.
Purpose: Examine the accuracy of an analysis involving spherical joints.
Summary: A homogeneous bar, pinned at a distance a from one end, with total length \(L\), is subjected to gravity loading and released from rest at an angle \(\theta=30\deg\) from the vertical. The rotational speed when it passes through \(\theta=0\deg\) is calculated and compared to an analytical expression.

The length of the spatial angular velocity vector at \(\theta=0\deg\) reads

\[\left|\omega\right|=\sqrt{\frac{0.402g_{3}\left(L-2a\right)}{L^{2}-3La+3a^{2}}}\]

provided the bar was released at \(\theta=30\deg\).

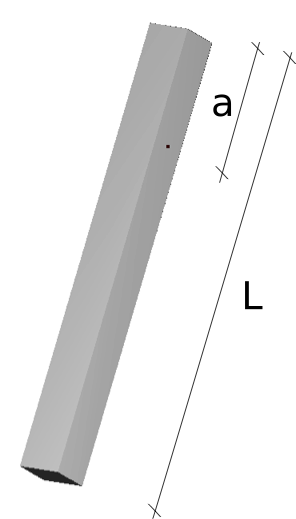
../../_images/pinned-bar.png

Fig. 15 The pinned bar in the initial configuration.

Input parameters

Density \(\left(kg/m^{3}\right)\)

\(\rho=1\)

Square cross-section \(\left(m^{2}\right)\)

\(b\times b=0.1\times0.1\)

Length \(\left(m\right)\)

\(L=1\)

Distance to joints \(\left(m\right)\)

\(a=0.25\)

Gravity acceleration \(\left(m/s^{2}\right)\)

\(\mathbf{g}=\left[0,0,-9.8\right]\)

Results

The time step used in the analysis is \(h=2^{-8}\). The hinge is modeled by a pair of spherical joints. The computations are terminated for the first n such that \(\theta\left(nh\right)\le0\) (interpolation of the results to the exact point \(\theta\left(t\right)=0\) is omitted). The table below summarizes the results

Target

Solfec-1.0

Ratio

Length of angular velocity when \(\theta=0\deg\,\, \left(rad/s\right)\)

2.121

2.116

0.997
../../_images/pinned-bar.gif

Fig. 16 Animation of the pinned bar (reload page or click on image to restart).