Projectile in a ballistic motion

Reference: J. B. Marion, S. T. Thornton, Classical Dynamics of Particles & Systems, 3rd Edition, Reference: Saunders College Publishing, 1988, pp. 60-63. Analysis: Explicit dynamics, unconstrained linear motion. Purpose: Examine the accuracy of integration of the linear motion. Summary: A projectile is subjected to gravity and air resistance loading. The total travel time and travel distance are calculated for an assumed initial velocity and air resistance proportionality constant, \(k\).

The air resistance force reads

\[\mathbf{f}_{air}=-km\mathbf{v}\]

where \(k\) is the resistance proportionality constant, \(m\) is the mass, and \(\mathbf{v}\) is the point mass velocity (nonzero in the \(x-z\) plane). The exact solution is

\[\begin{split}\mathbf{x}\left(t\right)=\left[\begin{array}{c} \frac{v_{1}\left(0\right)}{k}\left(1-\exp\left(-kt\right)\right)\\ 0\\ \frac{-g_{3}t}{k}+\frac{kv_{3}\left(0\right)+g_{3}}{k^{2}}\left(1-\exp\left(-kt\right)\right) \end{array}\right]\end{split}\]

where \(g_{3}\) is the vertical component of the gravity acceleration vector \(\mathbf{g}\). The travel time from the ground level \(x_{3}\left(0\right)=0\) until \(x_{3}\left(T\right)=0\) is given by

(94)\[T=\frac{hv_{3}\left(0\right)+g_{3}}{g_{3}k}\left(1-\exp\left(-kT\right)\right)\]

Input parameters

Mass \(\left(kg\right)\)	\(m=0.45359237\)
Initial linear velocity \(\left(m/s\right)\)	\(\mathbf{v}=\left[2.54,0,12.7\right]\)
Gravity acceleration \(\left(m/s^{2}\right)\)	\(\mathbf{g}=\left[0,0,-9.81456\right]\)
Proportionality constant	\(k=1\)

Results

The solution of equation (94) is \(T=1.976\) seconds. The time step used in the analysis was \(h=T/1024\). The table below and Fig. 14 summarise the results.

	Target	Solfec-1.0	Ratio
Travel time for projectile \(\left(s\right)\)	1.9760	1.9760	1.000
\(x\)-direction travel distance \(\left(in\right)\)	86.138	86.081	0.999

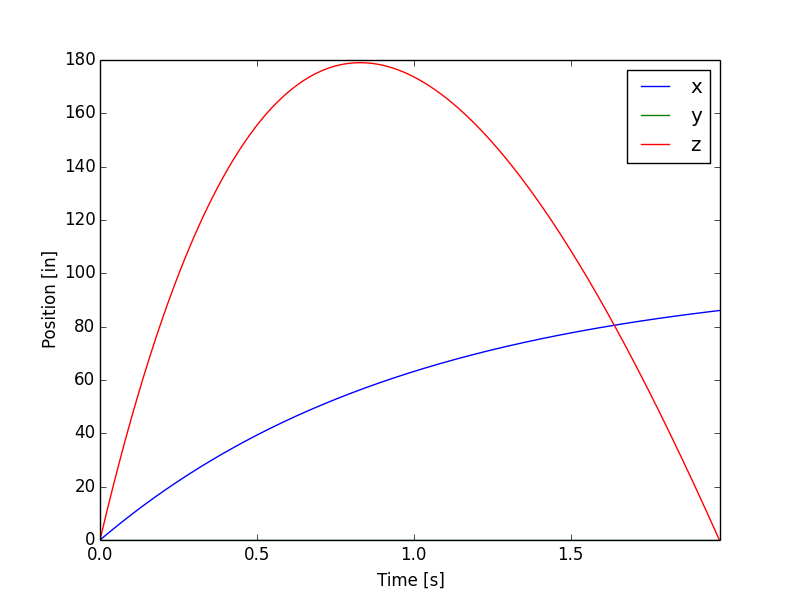
Fig. 14 Displacement of projectile over time.